7. Movimiento

7.3. Movimiento ondulatorio

En ocasiones, podemos querer crear movimientos más sutiles de oscilación; es aquí cuando necesitaremos repasar un poco de trigonometría, ya que haremos uso de las funciones seno y coseno que nos ofrece P5.js, sin() y cos().

Si tomamos como referencia un círculo de una unidad de radio (círculo unitario), tanto el seno como el coseno de un ángulo no son más que valores que oscilan entre –1 y 1 a medida que el valor del ángulo del círculo aumenta o disminuye.

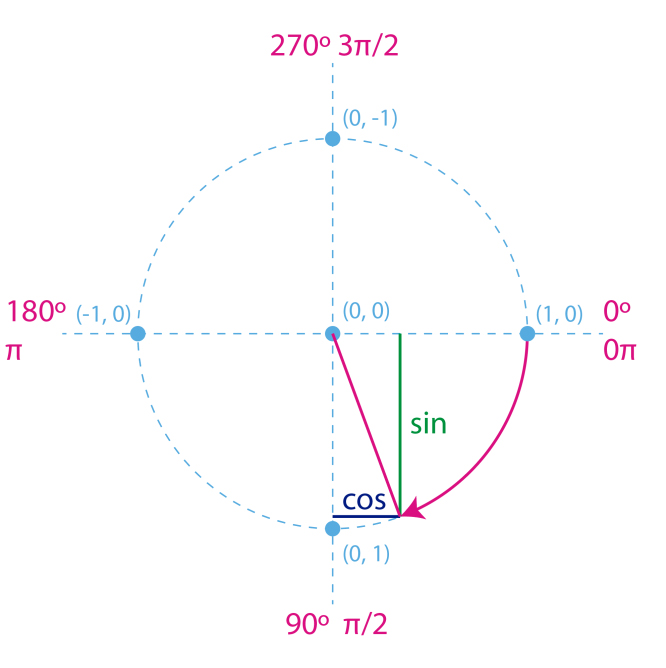
Recordemos que en P5 se trabaja por defecto con los ángulos en radianes y no en grados, y que el sentido positivo es en la dirección de las agujas del reloj y no al contrario (ya que nuestras coordenadas y en nuestro canvas crecen hacia abajo). De esta manera, podemos establecer el seno y coseno siguiendo la siguiente figura:

Vemos que comenzando en 0º (0 radianes), el seno va aumentando hasta llegar a un valor de 1 al alcanzar los 90º (PI/2 en radianes, HALF_PI en P5). A continuación, va disminuyendo hasta 0 al alcanzar los 180º (PI), sigue disminuyendo hasta –1 cuando alcanza los 270º (PI + HALF_PI) y luego aumenta hasta llegar de nuevo a 0 cuando el ángulo alcanza los 360º (TWO_PI). El coseno para 0º empieza con un valor de 1, disminuye hasta –1 en los 180º y aumenta hasta 1 de nuevo en los 360º.

Ángulo en grados	Ángulo en radianes	Seno	Coseno
0 o 360	0 o 2 × PI	0	1
90	PI / 2	1	0
180	PI	0	–1
270	3 × PI / 2	–1	0

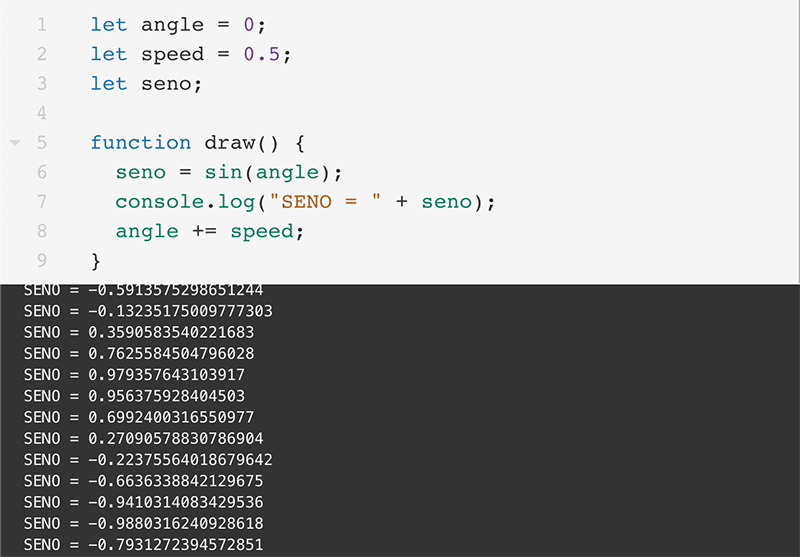
Si tenemos un valor de ángulo que vaya aumentado constantemente, su seno o su coseno variarán constantemente también entre –1 y 1, lo cual nos puede resultar muy útil. Veamos un ejemplo sencillo construido en P5.js:

Podemos observar que efectivamente los valores que nos devuelve sin() fluctúan entre –1 y 1 según vamos aumentando el valor del ángulo. Veamos ahora cómo podemos utilizar estos valores para controlar el movimiento de un círculo:

Como ya sabemos que los valores que sin() nos va a devolver van a oscilar entre –1 y 1, podemos usar el método map() para ajustar ese rango al rango del movimiento que queramos darle a nuestra figura; en este caso del rango (–1, 1) pasamos a (50, 350).