7.3. Moviment ondulatori
A vegades, podem voler crear moviments més subtils d’oscil·lació; és aquí quan necessitarem repassar una mica de trigonometria, ja que farem ús de les funcions sinus i cosinus que ens ofereix P5.js, sin() i cos().
Si prenem com a referència un cercle d’una unitat de ràdio (cercle unitari), tant el sinus com el cosinus d’un angle no són més que valors que oscil·len entre –1 i 1 a mesura que el valor de l’angle del cercle augmenta o disminueix.
Recordem que en P5 es treballa per defecte amb els angles en radiants i no en graus, i que el sentit positiu és en la direcció de les agulles del rellotge i no al contrari (ja que les nostres coordenades y en el nostre canvas creixen cap avall). D’aquesta manera, podem establir el sinus i cosinus seguint la figura següent:
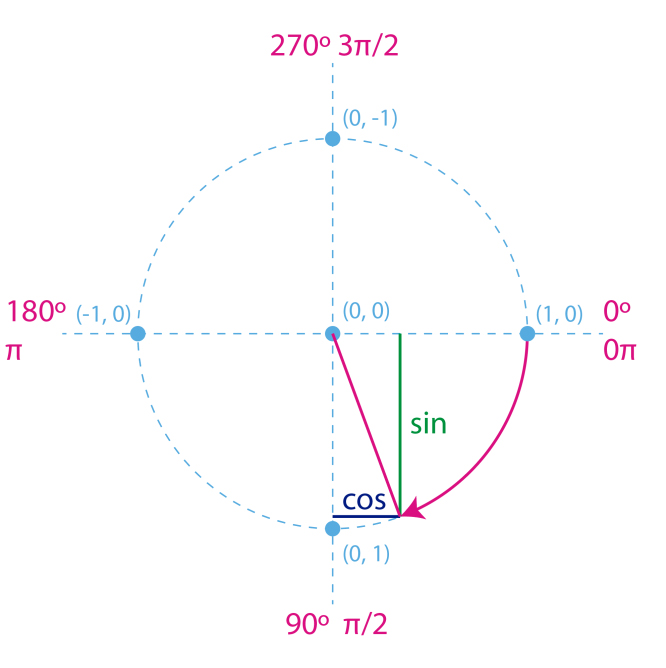
Font: elaboració pròpia.
Veiem que començant en 0° (0 radiants), el sinus va augmentant fins a arribar a un valor d’1 en assolir els 90° (PI/2 en radiants, HALF_PI en P5). A continuació, va disminuint fins a 0 en assolir els 180° (PI), continua disminuint fins a –1 quan assoleix els 270° (PI + HALF_PI) i després augmenta fins arribar de nou a 0 quan l’angle assoleix els 360° (TWO_PI). El cosinus per 0° comença amb un valor d’1, disminueix fins a –1 en els 180° i augmenta fins a 1 de nou en els 360°.
Tabla 3. Valors de sinus i cosinus
| Angle en graus | Angle en radiants | Sinus | Cosinus |
| 0 o 360 | 0 o 2 × PI | 0 | 1 |
| 90 | PI / 2 | 1 | 0 |
| 180 | PI | 0 | –1 |
| 270 | 3 × PI / 2 | –1 | 0 |
Si tenim un valor d’angle que vagi augmentat constantment, el seu sinus o el seu cosinus variaran constantment també entre –1 i 1, la qual cosa ens pot resultar molt útil. Vegem-ne un exemple senzill construït en P5.js:
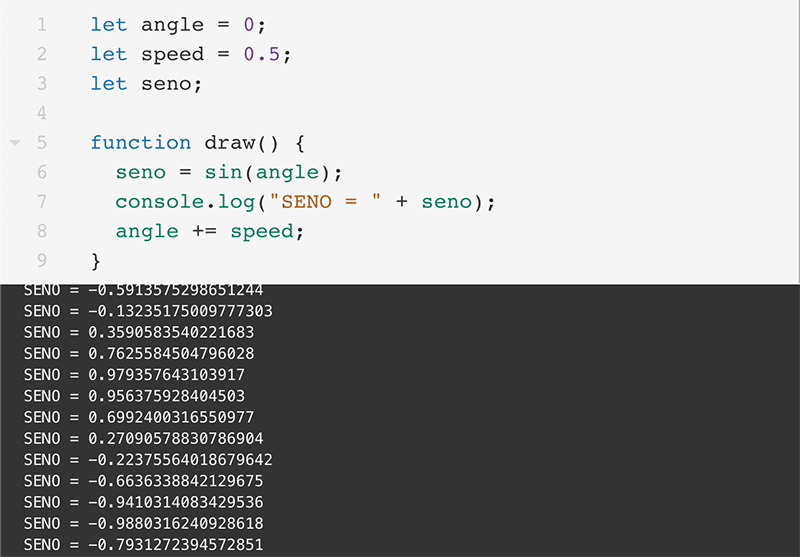
Font: elaboració pròpia.

Font: elaboració pròpia.